Table Of Contents
- 4. Python Hacks
Previous topic
Next topic
This Page
Quick search
Enter search terms or a module, class or function name.
This part is reserved for code that might be helpful in the process of doing financial calculations.
| download: | the calculationtree module |
|---|
The code is open source under the Python Software Foundation License
Abstract:
I got very much inspired when seeing a code note on how to build spreadsheets in Python
What the author really does is to show how to use the eval function to evaluate a set of formulas, some of them hierachical.
So this code is about answering the questions:
When a set of formulas is build it is often wanted to hide some of the formulas. In spreadsheets this can be handled by:
- show/hide columns and rows
- Spreadsheet design by dividing sheets into presentation, calculation and input sheets
- The use of constants, ie named variables not presented in a cell
When a set of formulas is build it is wanted to use the set as a function repeatedly. In spreadsheets this can be handled by:
- Use of scenarios
- Use of what-if
Off course the answers to the above depends on what you want to do. The idea here is to create an abstract data type to use for building and testing eg binomial trees and finite difference methods for option pricing in finance.
The prototype is the calculation tree below.
A calculationTree is build of branches or leafs, who has a key and a value. The value is either a formula (class) for a branch or a number (class) for a leaf. A branch is refered to by another branch if the key of the first branch is in the formula of the second branch. A root is a branch not refered to by any other branches. If a calculationTree is all leafs there vill be no roots.
The tree can’t be circular.
The definition of a calculation tree and adding formulas and values:
>>> ct = calculationTree()
>>> ct['a1'] = '5'
>>> ct['a2'] = '= a1*6'
>>> ct['a3'] = '= a2*7 + a1'
Evaluating formulas:
>>> ct['a3']
215
>>> ct['a2']
30
>>> ct['b1'] = '= sin(pi/4)'
>>> ct['b1']
0.70710678118654746
Showing a formula:
>>> ct.getformula('b1')
'= sin(pi/4)'
No circular references is allowed:
>>> try:
... ct['a1'] = '= a2'
... except Exception, errorTxt:
... print errorTxt
...
Circular reference
There is check for trees not ending in leafs:
>>> ct['a5'] = '= a4'
>>> ct['a5']
'key(a4) is not evaluable'
>>> ct['a6']
'key(a6) is not evaluable'
Getting the roots:
>>> ct.getRoots()
['a3', 'b1', 'a5']
Another way seeing the roots and their values:
>>> print ct
Roots for calculation tree:
* a3 = 215
* b1 = 0.707106781187
* a5 = key(a4) is not evaluable
Find formulas containing a specific key:
>>> print ct.findKeyInFormulas('a4')
Key(a4) is in the following formulas
a5 = a4
Showing the evalation tree below a branch:
>>> print ct.showEvaluation('a3')
|_ a3 = a2*7 + a1 (215)
|_ a1 = 5 (5)
|_ a2 = a1*6 (30)
|_ a1 = 5 (5)
>>> print ct.showEvaluation('b1')
|_ b1 = sin(pi/4) (0.707106781187)
It has been decided to use the datatype Decimal as base for al calculations in the finance package.
There are 2 reasons for this:
See also the chapter that examplifies the reasons for this.
The Package decimalpy is inspired by numpy and eg the vector concept of The R package. The key difference from numpy is that in decimalpy the only Decimal type is decimal.
The Package contains:
The package will be extended in order to support the needs in the package finance .
The finance package is open source under the Python Software Foundation License
If value can be converted to a Decimal type then the decimal version of value is returned. This function becomes obsolete as soon as decimalpy get’s it’s own Decimal type.
Usage
>>> from decimal import Decimal
>>> to_decimal(Decimal('4.5')), to_decimal('4.5'), to_decimal(4.5)
(Decimal('4.5'), Decimal('4.5'), Decimal('4.5'))
Rounds off Decimal by nbr_of_decimals using rounding_method. Decimal should be used whenever one is doing financial calculations. Decimal avoids small errors due Decimal representation etc. In other words calculations become similar to those in spreadsheets like eg Excel.
Generates nbr_of_steps step values starting with min and ending with max, both included.
Usage
>>> ['%.3f' % step for step in linspace_iter(2, 3, 5)]
['2.000', '2.250', '2.500', '2.750', '3.000']
An abstract datatype integrating the qualities of numpy’s array and the class decimal.s
How to use
>>> cf = Vector(5, 0.1)
>>> cf[-1] += 1
>>> cf
Vector([0.1, 0.1, 0.1, 0.1, 1.1])
>>> times = Vector(range(1,6))
>>> discount = Decimal('1.1') ** - times
>>> sum(discount * cf) # Present value
Decimal('1.000000000000000000000000000')
>>> discount(cf) # Present value by dot product
Decimal('1.000000000000000000000000000')
>>> sum(cf * Decimal('1.1') ** - times) # Present value
Decimal('1.000000000000000000000000000')
>>> cf(Decimal('1.1') ** - times) # Present value by dot product
Decimal('1.000000000000000000000000000')
>>> sum(cf / Decimal('1.1') ** times) # Present value
Decimal('1.000000000000000000000000000')
>>> times[:4] - times[1:]
Vector([-1, -1, -1, -1])
L.append(object) – append object to end
L.extend(iterable) – extend list by appending elements from the iterable
Raises ValueError if the value is not present.
L.insert(index, object) – insert object before index
Raises IndexError if list is empty or index is out of range.
L.remove(value) – remove first occurrence of value. Raises ValueError if the value is not present.
L.reverse() – reverse IN PLACE
L.sort(cmp=None, key=None, reverse=False) – stable sort IN PLACE; cmp(x, y) -> -1, 0, 1
SortedKeysDecimalValuedDict is a generalisation of Vector. The later is a SortedKeysDecimalValuedDict where the keys are consequtive integers starting with zero.
In SortedKeysDecimalValuedDict the keys can be any ordered set of elements of the same type.
The values are off course still Decimals. And the vectorlike functionality is still valid if the keys are of the same type.
Arguments at instantiation should be:
The type setting of keys can be defined at the static method __validate_key__ which has to return an validated value if possible. Otherwise it has to return the value None.
So to create a SortedKeysDecimalValuedDict with keys converted to strings eg just do:
>>> class string_based_Vector(SortedKeysDecimalValuedDict):
... @staticmethod
... def __validate_key__(key):
... return str(key)
Now any attempted key is converted to it’s string representation.
How to use
>>> class TimeFlow(SortedKeysDecimalValuedDict):
... @staticmethod
... def __validate_key__(key):
... return SortedKeysDecimalValuedDict.__validate_value__(key)
...
>>> cf = TimeFlow(Vector(5, 0.1))
>>> cf[4] += 1 # This is not the index 4, but the key 4
>>> cf
Data for the TimeFlow:
* key: 0, value: 0.1
* key: 1, value: 0.1
* key: 2, value: 0.1
* key: 3, value: 0.1
* key: 4, value: 1.1
>>> times = TimeFlow(Vector(range(1,6)))
>>> -times
Data for the TimeFlow:
* key: 0, value: -1
* key: 1, value: -2
* key: 2, value: -3
* key: 3, value: -4
* key: 4, value: -5
>>> discount = Decimal('1.1') ** - times
>>> discount
Data for the TimeFlow:
* key: 0, value: 0.9090909090909090909090909091
* key: 1, value: 0.8264462809917355371900826446
* key: 2, value: 0.7513148009015777610818933133
* key: 3, value: 0.6830134553650706918926302848
* key: 4, value: 0.6209213230591551744478457135
>>> present_values = discount * cf
>>> sum(present_values.values()) # Present value
Decimal('1.000000000000000000000000000')
v defaults to None.
If key is not found, d is returned if given, otherwise KeyError is raised
2-tuple; but raise KeyError if D is empty.
If E present and has a .keys() method, does: for k in E: D[k] = E[k] If E present and lacks .keys() method, does: for (k, v) in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k]
Polynomials has exponents as integers and factors as decimals.
It uses an extended Horners method for evaluation. And derivatives can found exact by specifying a degree of differention.
The price paid for this extension is that PolyExponents can only have positive arguments.
At instantiation:
| Parameters: | dct_of_exponents_and_factors (A dictionary where the keys are exponents and the values are factors.) – Array of x-coordinates |
|---|
When called as a function
| Parameters: | base_value (A Decimal (Integer, float or Decimal)) – Specifying the degree of differention |
|---|---|
| Returns: | When called as a function returns the functional value. If a degree is specified then the degree order derivative is returned |
How to use:
Let’s start with a simple polynomial: 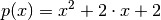 .
Then the dct_of_exponents_and_factors is {2:1, 1:2, 0:2}.
The dct_of_exponents_and_factors of the first derivative is {1:2, 0:2}.
And the dct_of_exponents_and_factors of the first derivative is {0:2}.
.
Then the dct_of_exponents_and_factors is {2:1, 1:2, 0:2}.
The dct_of_exponents_and_factors of the first derivative is {1:2, 0:2}.
And the dct_of_exponents_and_factors of the first derivative is {0:2}.
Instantiation is done as:
>>> pe = Polynomial({2:1, 1:2, 0:2})
>>> print pe
<Polynomial(x^2 + 2 x + 2)>
>>> pe
<Polynomial(x^2 + 2 x + 2)>
>>> pe.derivative()
<Polynomial(2 x + 2)>
>>> pe.derivative().derivative()
<Polynomial(2)>
>>> pe.derivative().integral()
<Polynomial(x^2 + 2 x)>
>>> pe.derivative().integral(-5)
<Polynomial(x^2 + 2 x - 5)>
>>> -pe
<Polynomial(- x^2 - 2 x - 2)>
>>> Polynomial({}), pe + (-pe), pe - pe
(<Polynomial(0)>, <Polynomial(0)>, <Polynomial(0)>)
>>> pe * 2
<Polynomial(2 x^2 + 4 x + 4)>
>>> pe + pe
<Polynomial(2 x^2 + 4 x + 4)>
>>> pe * pe
<Polynomial(x^4 + 4 x^3 + 8 x^2 + 8 x + 4)>
>>> pe ** 2
<Polynomial(x^4 + 4 x^3 + 8 x^2 + 8 x + 4)>
>>> Polynomial({1:1, 0:1}) ** 5
<Polynomial(x^5 + 5 x^4 + 10 x^3 + 10 x^2 + 5 x + 1)>
Get function value at x = -1 and 1 and the first order derivative and second order derivative at x = 1:
>>> pe([-1, 1]), pe.derivative()(1), pe.derivative().derivative()(1)
(Vector([1, 5]), Decimal('4'), Decimal('2'))
>>> pe[1] = 0
>>> pe
<Polynomial(x^2 + 2)>
>>> pe = Polynomial({1:1, 0:1}) ** 3
>>> pe(2)
Decimal('27')
>>> pe.inverse(27)
Decimal('2.000000000000000000000000000')
>>> pe = Polynomial({2:1, 1:1}) ** 2
>>> pe(2)
Decimal('36')
>>> pe =Polynomial({0:1, -1:1, -2:1, 1:2})
>>> pe
<Polynomial(2 x + 1)>
>>> pe(2)
Decimal('5')
v defaults to None.
If key is not found, d is returned if given, otherwise KeyError is raised
2-tuple; but raise KeyError if D is empty.
If E present and has a .keys() method, does: for k in E: D[k] = E[k] If E present and lacks .keys() method, does: for (k, v) in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k]
PolyExponents are an extension of polynomials. Here the exponents doesn’t have to be just integers. All decimal type values are accepted as exponents. So it is fair to say that a PolyExponents is a linear combination of roots, negative and positive powers.
It uses an extended Horners method for evaluation. And derivatives can found exact by specifying a degree of differention.
The price paid for this extension is that PolyExponents can only have positive arguments.
At instantiation:
| Parameters: | dct_of_exponents_and_factors (A dictionary where the keys are exponents and the values are factors.) – Array of x-coordinates |
|---|
When called as a function
| Parameters: | base_value (A Decimal (Integer, float or Decimal)) – Specifying the degree of differention |
|---|---|
| Returns: | When called as a function returns the functional value. If a degree is specified then the degree order derivative is returned |
How to use:
Use PolyExponents in financial calculations. First construct the npv as a function of 1 + r
>>> from decimalpy import Vector, PolyExponents
>>> cf = Vector(5, 0.1)
>>> cf[-1] += 1
>>> cf
Vector([0.1, 0.1, 0.1, 0.1, 1.1])
>>> times = Vector(range(0,5)) + 0.783
>>> times_and_payments = dict(zip(-times, cf))
>>> npv = PolyExponents(times_and_payments, '(1+r)')
>>> npv
<PolyExponents(0.1 (1+r)^-0.783 + 0.1 (1+r)^-1.783 + 0.1 (1+r)^-2.783 + 0.1 (1+r)^-3.783 + 1.1 (1+r)^-4.783)>
>>> try:
... npv(-1)
... except Exception, error_text:
... print error_text
Only non-negative arguments are allowed
* variable_index=1
* args=(<PolyExponents(0.1 (1+r)^-0.783 + 0.1 (1+r)^-1.783 + 0.1 (1+r)^-2.783 + 0.1 (1+r)^-3.783 + 1.1 (1+r)^-4.783)>, -1)
* kwargs={}
* argument_is_decimal=False
Get the npv at rate 10%, ie 1 + r = 1.1:
>>> OnePlusR = 1.1
>>> npv(OnePlusR)
Decimal('1.020897670129900750434884605')
Now find the internal rate, ie npv = 1 (note that default starting value is 0, which isn’t a good starting point in this case. A far better starting point is 1 which is the second parameter in the call of method inverse):
>>> npv.inverse(1, 1) - 1
Decimal('0.105777770945873634162979715')
So the internal rate is approximately 10.78%
Now let’s add some discountfactors, eg reduce with 5% p.a.:
So the discount factors are:
>>> discount = Decimal('1.05') ** - times
And the discounted cashflows are:
>>> disc_npv = npv * discount
>>> disc_npv
<PolyExponents(0.09625178201551631581068644778 x^-0.783 + 0.09166836382430125315303471217 x^-1.783 + 0.08730320364219166966955686873 x^-2.783 + 0.08314590823065873301862558927 x^-3.783 + 0.8710523719402343459094109352 x^-4.783)>
And the internal rate is:
>>> disc_npv.inverse(1, 1) - 1
Decimal('0.053121686615117746821885443')
And now it is seen that the internal rate is a multiplicative spread:
>>> disc_npv.inverse(1, 1) * Decimal('1.05') - 1
Decimal('0.105777770945873634162979715')
which is the same rate as before.
v defaults to None.
If key is not found, d is returned if given, otherwise KeyError is raised
2-tuple; but raise KeyError if D is empty.
If E present and has a .keys() method, does: for k in E: D[k] = E[k] If E present and lacks .keys() method, does: for (k, v) in E: D[k] = v In either case, this is followed by: for k in F: D[k] = F[k]
A decorator to convert python functions to numpy universal functions
A standard function of 1 variable is extended by a decorator to handle all values in a list or tuple
| Parameters: | variable_index (An positive integer) – Specifies index for args to use as variable. This way the function can be used in classes as well as functions |
|---|
How to use:
In the example below vector_function is used on the first parameter x:
>>> from decimal import Decimal
>>> @vector_function(0)
... def test(x, y=2):
... return x+y
...
>>> x0 = 4
>>> x1 = (1, float(2), Decimal('3'))
>>> x2 = [2, 3, 4]
>>> x3 = Vector(x1) + 2
>>> test(x0)
Decimal('6')
>>> print test(x1)
Vector([3, 4.0, 5])
>>> print test(x2)
Vector([4, 5, 6])
>>> print test(x3)
Vector([5, 6.0, 7])
Note that since argument y has a default value 2 it isn’t set in the function call. So these are not handled by the vector_function. To see this do:
>>> @vector_function(1)
... def test(x, y=2):
... return x+y
...
>>> try:
... test(1)
... except Exception, error_tekst:
... print error_tekst
...
tuple index out of range
* variable_index=1
* args=(1,)
* kwargs={}
* argument_is_decimal=False
In the example above args is a tuple of length 1, we want’s to let the vector_function work on argument Decimal 2 at position 1, but there are no argument Decimal 2 in the call.
However the call below works just fine:
>>> test(1, (1, float(2), Decimal('3')))
Vector([2, 3.0, 4])
It is just that the value has to be set in the function call in order to have vector_function working. Therefore setting a default value make’s no sense.
If argument_is_decimal is True it means that the argument is transformed into a Decimal if possible else the value is returned.
>>> @vector_function(0)
... def test(x):
... return 2/x
...
>>> test(3)
Decimal('0')
Here the division becomes integer part division since the argument is an integer and hence both nominator and denominator are integers.
If on the other hand argument_is_decimal is True the argument becomes a Decimal and division becomes division between real Decimals as shown below:
>>> @vector_function(0, True)
... def test(x):
... return 2/x
...
>>> test(3)
Decimal('0.6666666666666666666666666667')
Remember that arguments at instantiation must be decimals. Hence use of the function Decimal in __init__
>>> class Test:
... def __init__(self, x):
... self.x = Decimal(x)
... @vector_function(1, True)
... def __call__(self, y):
... return self.x * y
...
>>> test = Test(2.)
>>> test([3., 6, 9])
Vector([6.0, 12, 18])
The exponetial function as a Vector function.
How to use
>>> x0 = 4
>>> x1 = (1, float(2), Decimal('3'))
>>> exp(x0)
Decimal('54.59815003314423907811026120')
>>> x1 = (1, float(2), Decimal('3'))
>>> exp(x1)
Vector([2.718281828459045235360287471, 7.389056098930650227230427461, 20.08553692318766774092852965])
The natural logarithmic function as a Vector function.
How to use
>>> ln(8)
Decimal('2.079441541679835928251696364')
>>> ln((1, float(2), Decimal('8')))
Vector([0, 0.6931471805599453094172321215, 2.079441541679835928251696364])
A piecewise constant function is constant on intervals on the x-axis. It is right contionous as well which means that a set of points can define the function since each point is the right most point from the previous point. First point is assumed prolonged to x = minus infinity and last point is prolonged to x = infinity
At instantiation:
| Parameters: |
|
|---|
When called as a function:
| Parameters: | x (A real number) – The value to interpolate from |
|---|
How to use:
>>> x_data = Vector([1, 3, 5])
>>> y_data = Vector([7, 9, 13])
>>> # Instantiation
>>> pc = PiecewiseConstant(x_data, y_data)
>>> pc
Piecewise constant curve based on points:
.. (1.0000, 7.0000)
.. (3.0000, 9.0000)
.. (5.0000, 13.0000)
>>> pc([0, 1, 2, 3, 4, 5, 6])
Vector([7, 7, 9, 9, 13, 13, 13])
A linear interpolation connects point by the strait line though the points. First point is assumed prolonged horizontally to x = minus infinity and last point is likewise prolonged to x = infinity
At instantiation:
| Parameters: |
|
|---|
When called as a function:
| Parameters: | x (A real number) – The value to interpolate from |
|---|
How to use:
>>> x_data = Vector([1, 3, 5])
>>> y_data = Vector([7, 9, 13])
>>> # Instantiation
>>> li = LinearSpline(x_data, y_data)
>>> li
Linear interpolation curve based on points:
.. (1.0000, 7.0000)
.. (3.0000, 9.0000)
.. (5.0000, 13.0000)
>>> li([0, 1, 2, 3, 4, 5, 6])
Vector([7, 7, 8.0, 9, 11.0, 13, 13])
Function class for doing natural cubic spline interpolation. A linear extrapolation is used outside the interval of the x-values.
At instantiation:
| Parameters: |
|
|---|
At instantion the class function is prepared to calculate y-values for x-values according to the natural cubic spline.
Extrapolation is linear from the endpoints with the slope like the one at the endpoint.
When called as a function:
| Parameters: |
|
|---|---|
| Returns: | The corresponding y-value for x value according to the natural cubic spline and the points from instatiation |
How to use:
[Kiusalaas] p. 119
>>> x_data = Vector([1, 2, 3, 4, 5])
>>> y_data = Vector([0, 1, 0, 1, 0])
>>> # Instantiation
>>> f = NaturalCubicSpline(x_data, y_data)
>>> # f is just called as a function
>>> print f(1.5), f(4.5)
0.7678571428571428571428571427 0.7678571428571428571428571427
>>> print f(1.5, 1), f(4.5, 1)
1.178571428571428571428571429 -1.178571428571428571428571428
>>> print f(1.5, 2), f(4.5, 2)
-2.142857142857142857142857142 -2.142857142857142857142857143
Call the function with a tuple, list or an array
>>> print f([1.5, 4.5])
Vector([0.7678571428571428571428571427, 0.7678571428571428571428571427])
>>> print f([1.5, 4.5], 1)
Vector([1.178571428571428571428571429, -1.178571428571428571428571428])
>>> print f([1.5, 4.5], 2)
Vector([-2.142857142857142857142857142, -2.142857142857142857142857143])
Reference:
A financial cubic spline differs from the natural cubic spline in that has zero slope instead of zero curvature at the endpoint to the right.
Is instantiated with a countinous derivable function and a possible step size (default = Decimal(‘0.0001’)) for the numerical differentiation.
How to use:
>>> import decimalpy as dp
>>> deriv_ln = dp.NumericalFirstOrder(dp.ln)
>>> for x in (1, float(2), Decimal('8')): # must be (1, 0.5, 0.125)
... print deriv_ln(x)
...
0.9999999999999999199999971433
0.49999999999999999749999975
0.1249999999999999999975558333
>>> isinstance(deriv_ln(4), Decimal)
True
References:
Is instantiated with a countinous derivable function and a possible step size (default = Decimal(‘0.0001’)) for the numerical differentiation.
How to use:
>>> import decimalpy as dp
>>> curvature = dp.NumericalSecondOrder(dp.ln)
>>> for x in (1, float(2), Decimal('4')): # must be (-1, -0.25, -0.0625)
... print curvature(x)
...
-0.9999999999999998666666641667
-0.2499999999999999978333333333
-0.06250000000000000009166666667
References:
Solver How to use:
>>> import decimalpy as dp
>>> f = lambda x: x*x
>>> numeric_sqrt = Solver(f)
>>> for x in [4, 9.0, Decimal('16')]:
... print numeric_sqrt(x, 1)
2.000000000000002158638110942
3.000000000000000000325260652
4.000000000000050672229330380
This package implements professional financial calculations.
The finance package is open source under the Python Software Foundation License
A class to implement (non generic) banking day calculations.
How to use!
BankDate could instantiated by a string of type yyyy-mm-dd, a python date or a BankDate itself:
>>> from datetime import date
>>> td = BankDate('2009-09-25')
>>> td
2009-09-25
>>> print BankDate(date(2009,9,25))
2009-09-25
>>> print BankDate(td)
2009-09-25
When instantiating default is today.
A BankDate can be added a number of years, months or days:
>>> print td.add_years(5)
2014-09-25
>>> print td.add_months(-3)
2009-06-25
>>> print td.add_days(14)
2009-10-09
The differences between 2 dates can also be found:
>>> print td.nbr_of_years('2014-09-25')
5
>>> print td.nbr_of_months('2009-06-25')
-3
>>> print td.nbr_of_days('2009-10-09')
14
Finding next banking day / BankDate:
>>> d = BankDate('2009-09-27')
>>> print d.find_next_banking_day(1, ['2009-09-28'])
2009-09-29
Finding previous banking day / BankDate:
>>> print d.find_next_banking_day(-1, ['2009-09-28'])
2009-09-25
It is also possible to adjust to nearest banking day:
>>> d = BankDate('2009-10-31')
>>> d.adjust_to_bankingday('Actual')
2009-10-31
>>> d.adjust_to_bankingday('Following')
2009-11-02
>>> d.adjust_to_bankingday('Previous')
2009-10-30
>>> d.adjust_to_bankingday('ModifiedFollowing')
2009-10-30
>>> BankDate('2009-11-02').adjust_to_bankingday('ModifiedPrevious')
2009-11-02
Using operator overload:
By using operator overload it is more simple to handle calculations with BankDates and TimePeriods. The last represented by its string representation.
>>> td = BankDate('2009-09-25')
>>> print td + '5y', '5y' + td
2014-09-25 2014-09-25
>>> print td - '3m', '-3m' + td
2009-06-25 2009-06-25
>>> print td +'2w', '2w' + td
2009-10-09 2009-10-09
>>> print td +'14d', '14d' + td
2009-10-09 2009-10-09
>>> td - (td + '2d')
-2
It is possible to do more complicated updates at once:
>>> t1, t2 = BankDate(date(2009,12,27)), BankDate('2009-09-27')
>>> print t1 + '3m' + '2y'
2012-03-27
>>> print t2-t1, t1-t2
-91 91
BankDates can be compared:
>>> td = BankDate('2009-09-28')
>>> print td
2009-09-28
>>> td <= BankDate('2009-09-28')
True
>>> td == BankDate('2009-09-28')
True
>>> td == BankDate('2009-09-27')
False
A BankDate can be added years, months or days and be updated to the new date
>>> d = BankDate('2009-09-30')
>>> d+='3m'
>>> print d
2009-12-30
Adds nbr_days days to the BankDate.
| Parameters: | nbr_days (int) – Number of days to be added |
|---|
Adds nbr_months months to the BankDate.
| Parameters: | nbr_months (int) – Number of months to be added |
|---|
Adds nbr_years years to the BankDate.
| Parameters: | nbr_years (int) – Number of years to be added |
|---|
Adjust to banking day according to date rolloing rule and list of holidays.
Reference: http://en.wikipedia.org/wiki/Date_rolling
| Parameters: |
|
|---|---|
| Returns: | Adjusted banking day |
A workingday can not be saturday or sunday.
| Parameters: |
|
|---|---|
| Returns: | Next or previous working day given a holidaylist. Return itself if not in weekend or a holiday |
| Return : | first day in month for this BankDate as BankDate |
|---|
Identifies if BankDate is ultimo
| Parameters: | date (BankDate) – date |
|---|---|
| Returns: | The number of days between this bankingday and a date |
| Parameters: | date (BankDate) – date |
|---|---|
| Returns: | The number of months between this bankingday and a date |
| Parameters: | date (BankDate) – date |
|---|---|
| Returns: | The number of years between this bankingday and a date |
An IMM date is the 3. wednesday in the months march, june, september and december
reference: http://en.wikipedia.org/wiki/IMM_dates
| Return : | Next IMM date for BankDate as BankDate |
|---|
Return last day of month for a given number of month.
| Parameters: | nbr_month (int) – Number of month |
|---|
| Parameters: | as_string (Boolean) – Return weekday as a number or a string |
|---|---|
| Return : | day as a string or a day number of week, 0 = Monday etc |
A TimePeriod is a string containing an (positive or negative) integer called count and a character like d(days), m(months) or y(years) called unit. It is used for handling generic time periods.
How to use!
Instantiation:
>>> x = TimePeriod('2y')
How to get get the string representation and the values count and unit:
>>> x, x.count, x.unit
(2y, 2, 'y')
Operator overload
By using operator overload it is possible to do TimePeriod calculations quite easy. A TimePeriod can be added or subtracted an integer (same unit is assumed):
>>> 5 + x, x - 5
(7y, -3y)
A period can be multiplied by an integer:
>>> x * 5, 5 * TimePeriod('2y') + TimePeriod('2y')
(10y, 12y)
TimePeriods can be compared, if they have the same unit:
>>> TimePeriod('2y') > TimePeriod('1y')
True
>>> TimePeriod('2y') < TimePeriod('1y')
False
>>> try:
... TimePeriod('2m') < TimePeriod('1y')
... except Exception, errorText:
... print errorText
...
Non comparable units (m) vs (y)
Integer part of TimePeriod.
Unit part [y(ears), m(onths) or d(ays)] of TimePeriod.
A class to implement different daycount methods and the related time convertions.
| Parameters: |
|
|---|---|
| Returns: | A date converted to a time (of type Decimal) in years |
When called as a function:
| Parameters: | date – A BankDate |
|---|---|
| Returns: | the date, the following date according to settings and the time in years as a float according to settings |
How to use!
>>> dtt = DateToTime(valuation_date = '2009-11-08')
>>> print dtt # To see (default) settings
Time Convertion:
Daycount method = act/365
Valuation date = 2009-11-08
>>> bd = BankDate('2009-11-08')
>>> dtt(bd + "365d")
Decimal('1')
>>> dtt360 = DateToTime('360/360', bd)
>>> print dtt360
Time Convertion:
Daycount method = 360/360
Valuation date = 2009-11-08
>>> dtt360(bd + "12m")
Decimal('1')
>>> dtt360(bd + "15m")
Decimal('1.25')
>>> dtt360 = DateToTime('360/360', bd)
>>> print dtt360
Time Convertion:
Daycount method = 360/360
Valuation date = 2009-11-08
>>> d = bd + "7d"
>>> dtt360(d.adjust_to_bankingday('Following'))
Decimal('0.02222222222222222222222222222')
>>> dtt360([bd + "12m", bd + '15m'])
Vector([1, 1.25])
Get valuation day
Reset or set Daycount method
| Parameters: | daycount_method (‘act/365’, ‘act/360’, ‘360/360’, ‘act/actISDA’) – Name of day count method. Default is act/365 |
|---|
Reset or set valuation day
Get valuation day
| Parameters: | enddate_or_integer – Either end_date or number of dates in daterange :type enddate_or_integer: A date or integer :param start_date: start_date for daterange iterations.
if enddate_or_integer is an integer:
if enddate_or_integer is a date:
How to use! The next 5 dates (period a year) from 2009-11-23. start_date is included. >>> for d in daterange_iter(5, '2009-11-23'):
... print d
...
2014-11-23
2013-11-23
2012-11-23
2011-11-23
2010-11-23
2009-11-23
Taking date rolling and holidays into account. >>> for d in daterange_iter(5, '2009-11-23', daterolling='Following', holidaylist=['2011-11-23']):
... print d, d.weekday(True)
...
2014-11-24 Mon
2013-11-25 Mon
2012-11-23 Fri
2011-11-24 Thu
2010-11-23 Tue
2009-11-23 Mon
Countdown (period a year) from the future 2014-11-23. start_date is included. >>> for d in daterange_iter(-5, '2014-11-23'):
... print d
...
2014-11-23
2013-11-23
2012-11-23
2011-11-23
2010-11-23
2009-11-23
Countdown (period a year) from the future 2014-11-23. start_date is not included, ie. the smallest date. >>> for d in daterange_iter(-5, '2014-11-23', keep_start_date = False):
... print d
...
2014-11-23
2013-11-23
2012-11-23
2011-11-23
2010-11-23
Countdown (period minus a year) from the future 2014-11-23. start_date is included. >>> for d in daterange_iter(5, '2014-11-23', '-1y'):
... print d
...
2014-11-23
2013-11-23
2012-11-23
2011-11-23
2010-11-23
2009-11-23
Both countdowns repeal each other. >>> for d in daterange_iter(-5, '2009-11-23', '-1y'):
... print d
...
2014-11-23
2013-11-23
2012-11-23
2011-11-23
2010-11-23
2009-11-23
|
||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
daterange_iter handles almost ultimo dates:
>>> for d in daterange_iter(-12, '2013-05-30', daterolling='ModifiedFollowing', step='3m'):
... print d, d.weekday(True)
...
2013-05-30 Thu
2013-02-28 Thu
2012-11-30 Fri
2012-08-30 Thu
2012-05-30 Wed
2012-02-28 Tue
2011-11-30 Wed
2011-08-30 Tue
2011-05-30 Mon
2011-02-28 Mon
2010-11-30 Tue
2010-08-30 Mon
2010-05-31 Mon
And daterange_iter handles ultimo dates:
>>> for d in daterange_iter(-12, '2013-05-31', daterolling='ModifiedFollowing', step='3m'):
... print d, d.weekday(True)
...
2013-05-31 Fri
2013-02-28 Thu
2012-11-30 Fri
2012-08-31 Fri
2012-05-31 Thu
2012-02-28 Tue
2011-11-30 Wed
2011-08-31 Wed
2011-05-31 Tue
2011-02-28 Mon
2010-11-30 Tue
2010-08-31 Tue
2010-05-31 Mon
| Parameters: |
|
|---|---|
| Returns: | number (integer) of steps from end_date down to start_date |
How to use!
>>> period_count('2012-11-30', '2009-11-23', '1y')
4
Daterange returns a sorted list of BankDates.
| Parameters: |
|
|---|
if enddate_or_integer is an integer:
| Returns: | A list of dates starting from start_date and enddate_or_integer steps forward |
|---|
if enddate_or_integer is a date:
| Returns: | A list of dates starting from enddate_or_integer and steps backward until start_date |
|---|
How to use!
Get the next 5 dates from 2009-11-23 with a time step of 1 year. start_date is included.
>>> daterange(5, '2009-11-23')
[2009-11-23, 2010-11-23, 2011-11-23, 2012-11-23, 2013-11-23, 2014-11-23]
Get the dates between 2009-11-23 and 2012-11-30 with a time step of 3 months. Start_date is not included.
>>> daterange('2010-11-30', '2009-11-23', '3m', False)
[2009-11-30, 2010-02-28, 2010-05-30, 2010-08-30, 2010-11-30]
Get the dates between 2009-11-23 and 2012-11-30 with a time step of 1 year. start_date is included.
>>> daterange('2012-11-30', '2009-11-23')
[2009-11-23, 2009-11-30, 2010-11-30, 2011-11-30, 2012-11-30]
Get the dates between 2009-11-23 and 2012-11-30 with a time step of 1 year. start_date is not included.
>>> daterange('2012-11-30', '2009-11-23', '1y', False)
[2009-11-30, 2010-11-30, 2011-11-30, 2012-11-30]
A DateFlow is a subclass SortedKeysDecimalValuedDict, where the keys are an list of bankdates and the values are of type decimal. Operator overload is used to simplify operations on DateFlows.
Operator overload principles
DateFlows can be added or subtracted to each other
- DateFlows can also be added, subtracted, multiplied or divided with
a number (float or int)
DateFlows can be ordered according to their date span
How to use!
The class DateFlow can be instantiated by a yyyy-mm-dd string, a Python date or a bankdate and possible a float or integer value. Default value is 0
>>> from datetime import date
>>> t1, t2, t3 = '2009-09-27', date(2009,12,27), BankDate('2009-09-27')
>>> c1, c2 = DateFlow({t1 : 100}), DateFlow({t2 : 200})
>>> c3 = DateFlow({t3 : 300})
>>> print c1
Data for the DateFlow:
* key: 2009-09-27, value: 100
>>> print c2
Data for the DateFlow:
* key: 2009-12-27, value: 200
>>> print c3
Data for the DateFlow:
* key: 2009-09-27, value: 300
2 or more DateFlows can be added. A DateFlow can also be added and multiplied with a number.
>>> print c1 + 2 * c2 + 1000
Data for the DateFlow:
* key: 2009-09-27, value: 1100
* key: 2009-12-27, value: 1400
When added DateFlows have dates in common the values are added on these dates.
>>> cf = c1 + 2 * c2 + c3 * 3 + 1000
>>> print cf
Data for the DateFlow:
* key: 2009-09-27, value: 2000
* key: 2009-12-27, value: 1400
It is possible to get the accumulated cashflow.
>>> cf.accumulated_dateflow()
Data for the DateFlow:
* key: 2009-09-27, value: 2000
* key: 2009-12-27, value: 3400
A DateFlow is a subclass of a dictionary and it can used accordingly.
>>> print cf['2009-12-27']
1400
>>> sorted(cf.keys())
[2009-09-27, 2009-12-27]
The method find_nearest_bankdate find the nearest bankdate equal to or below the input. Before if the second parameter before is True (default) otherwise the nearest date after).
>>> cf.find_nearest_bankdate('2009-08-06')
>>> cf.find_nearest_bankdate('2009-11-06')
2009-09-27
>>> cf.find_nearest_bankdate('2009-09-27')
2009-09-27
>>> cf.find_nearest_bankdate('2010-11-06')
2009-12-27
last_key returns the biggest bankdate in the cashflow
>>> end_date = (c1 + 2 * c2 + c3 * 3 + 1000).last_key()
>>> print end_date
2009-12-27
>>> print end_date - BankDate('2009-09-27')
91
A zero element for a DateFlow is similar to an empty dictionary.
>>> DateFlow({})
Data for the DateFlow:
*
A dictionary (of proper format) or a DateFlow can be used as initiation.
>>> y = DateFlow({'2009-09-11':100})
>>> DateFlow(y)
Data for the DateFlow:
* key: 2009-09-11, value: 100
DateFlows can be sliced by dates as well. Key must be a bankdate or a slice object.
Example
Look at an annuity starting 2010-04-26 running with 10 payments.
>>> x=dateflow_generator(0.1, 10, '2010-04-26')
>>> x
Data for the DateFlow:
* key: 2010-04-26, value: 0.0
* key: 2011-04-26, value: 16.2745394883
* key: 2012-04-26, value: 16.2745394883
* key: 2013-04-26, value: 16.2745394883
* key: 2014-04-26, value: 16.2745394883
* key: 2015-04-26, value: 16.2745394883
* key: 2016-04-26, value: 16.2745394883
* key: 2017-04-26, value: 16.2745394883
* key: 2018-04-26, value: 16.2745394883
* key: 2019-04-26, value: 16.2745394883
* key: 2020-04-26, value: 16.2745394883
The payments from 2018-04-22 and out is:
>>> x['2018-04-22':]
Data for the DateFlow:
* key: 2018-04-26, value: 16.2745394883
* key: 2019-04-26, value: 16.2745394883
* key: 2020-04-26, value: 16.2745394883
The payments between 2013-01-01 and 2017-01-01 is:
>>> x['2013-01-01':'2017-01-01']
Data for the DateFlow:
* key: 2013-04-26, value: 16.2745394883
* key: 2014-04-26, value: 16.2745394883
* key: 2015-04-26, value: 16.2745394883
* key: 2016-04-26, value: 16.2745394883
There are no payments between 2022-01-01 and 2032-01-01:
>>> x['2022-01-01':'2032-01-01']
Data for the DateFlow:
*
>>>
| Returns: | The accumulated DateFlow |
|---|
| Parameters: |
|
|---|---|
| Return : | The nearest date in DateFlow (before if before is True otherwise the nearest after) keyvalue. |
A generator of standard DateFlows.
Steps step backwards from end_date. If enddate_or_integer is an integer
end_date is calculated as start_date + enddate_or_integer * step
The dateflow_generator is build upon the datarangeiter.
| Parameters: |
|
|---|
Create payments of an annuity with nominal 100, a rate of 10% and 5 yearly payments starting from 2009-11-24.
>>> dateflow_generator(0.1, 5, '2009-11-24')
Data for the DateFlow:
* key: 2009-11-24, value: 0.0
* key: 2010-11-24, value: 26.3797480795
* key: 2011-11-24, value: 26.3797480795
* key: 2012-11-24, value: 26.3797480795
* key: 2013-11-24, value: 26.3797480795
* key: 2014-11-24, value: 26.3797480795
DateFlow can also be generated from the future and back:
>>> dateflow_generator(0.1, -5, '2014-11-24')
Data for the DateFlow:
* key: 2009-11-24, value: 0.0
* key: 2010-11-24, value: 26.3797480795
* key: 2011-11-24, value: 26.3797480795
* key: 2012-11-24, value: 26.3797480795
* key: 2013-11-24, value: 26.3797480795
* key: 2014-11-24, value: 26.3797480795
Several DateFlows can be uptained. Below are the nominals of an annuity (default):
>>> dateflow_generator(0.1, 5, '2009-11-24', profile = 'nominal')
Data for the DateFlow:
* key: 2009-11-24, value: 100.0
* key: 2010-11-24, value: 83.6202519205
* key: 2011-11-24, value: 65.6025290331
* key: 2012-11-24, value: 45.7830338569
* key: 2013-11-24, value: 23.9815891632
* key: 2014-11-24, value: 0.0
And the rates of of an annuity (default):
>>> dateflow_generator(0.1, 5, '2009-11-24', profile = 'rate')
Data for the DateFlow:
* key: 2009-11-24, value: 0.0
* key: 2010-11-24, value: 10.0
* key: 2011-11-24, value: 8.36202519205
* key: 2012-11-24, value: 6.56025290331
* key: 2013-11-24, value: 4.57830338569
* key: 2014-11-24, value: 2.39815891632
Create the payments of a bullit with nominal 100, a rate of 10% and 5 yearly payments starting from 2009-11-24.
>>> dateflow_generator(0.1, 5, '2009-11-24', cashflowtype= 'bullit')
Data for the DateFlow:
* key: 2009-11-24, value: 0.0
* key: 2010-11-24, value: 10.0
* key: 2011-11-24, value: 10.0
* key: 2012-11-24, value: 10.0
* key: 2013-11-24, value: 10.0
* key: 2014-11-24, value: 110.0
Create the payments a series with nominal 100, a rate of 10% and 5 yearly payments starting from 2009-11-24.
>>> dateflow_generator(0.1, 5, BankDate('2009-11-24'), cashflowtype= 'series')
Data for the DateFlow:
* key: 2009-11-24, value: 0.0
* key: 2010-11-24, value: 30.0
* key: 2011-11-24, value: 28.0
* key: 2012-11-24, value: 26.0
* key: 2013-11-24, value: 24.0
* key: 2014-11-24, value: 22.0
[Christensen] table 2.3 page 30, payments:
>>> dateflow_generator(0.035, '2004-07-01', '2001-01-01', '6m', 'annuity', 'payment')
Data for the DateFlow:
* key: 2001-01-01, value: 0.0
* key: 2001-07-01, value: 16.3544493783
* key: 2002-01-01, value: 16.3544493783
* key: 2002-07-01, value: 16.3544493783
* key: 2003-01-01, value: 16.3544493783
* key: 2003-07-01, value: 16.3544493783
* key: 2004-01-01, value: 16.3544493783
* key: 2004-07-01, value: 16.3544493783
[Christensen] table 2.3 page 30, rates:
>>> dateflow_generator(0.035, '2004-07-01', '2001-01-01', '6m', 'annuity', 'rate')
Data for the DateFlow:
* key: 2001-01-01, value: 0.0
* key: 2001-07-01, value: 3.5
* key: 2002-01-01, value: 3.05009427176
* key: 2002-07-01, value: 2.58444184303
* key: 2003-01-01, value: 2.10249157929
* key: 2003-07-01, value: 1.60367305633
* key: 2004-01-01, value: 1.08739588506
* key: 2004-07-01, value: 0.553049012794
[Christensen] table 2.3 page 30, nominals:
>>> dateflow_generator(0.035, '2004-07-01', '2001-01-01', '6m', 'annuity', 'nominal')
Data for the DateFlow:
* key: 2001-01-01, value: 100.0
* key: 2001-07-01, value: 87.1455506217
* key: 2002-01-01, value: 73.8411955151
* key: 2002-07-01, value: 60.0711879798
* key: 2003-01-01, value: 45.8192301808
* key: 2003-07-01, value: 31.0684538588
* key: 2004-01-01, value: 15.8014003655
* key: 2004-07-01, value: 0.0
Timeflow combines the logic of DateToTime and yieldcurves to transform a dateflow though discounting into something that have eg a present value, derivatives and a spread. DateToTime transform dates to time and yieldcurves weigths the payments.
Usage
A DateToTime is needed to define the conversion from date to time.
>>> from finance.timeflow import DateToTime
>>> dtt = DateToTime(valuation_date = '2009-11-22')
Instantiate with DateToTime object alone:
>>> from finance import TimeFlow
>>> tf = TimeFlow(dtt)
>>> tf
<instance TimeFlow>
Time Convertion:
Daycount method = act/365
Valuation date = 2009-11-22
Specify a DateFlow to use:
>>> from finance import DateFlow
>>> df = DateFlow({BankDate('2010-11-12') : 453})
The DateFlow can be added like:
>>> tf.dateflow = df
>>> tf
<instance TimeFlow>
Time Convertion:
Daycount method = act/365
Valuation date = 2009-11-22
Or the DateFlow can be added at instatiation like:
>>> tf = TimeFlow(dtt, dateflow=df)
>>> print tf
<instance TimeFlow>
Time Convertion:
Daycount method = act/365
Valuation date = 2009-11-22
Date Time Value
2009-11-22, 0.0000, 0.00
2010-11-12, 0.9726, 453.00
Let’s have amore interesting example. Let’s look at a bullit cashflow defined to start at 2009-11-24, having 5 rate payments of 10% and with a repayment of the nominal at the last rate payment.
First use the dateflow_generator to generate the bullit cashflow:
>>> from finance import dateflow_generator
>>> df = dateflow_generator(0.1, 5, '2009-11-24', cashflowtype='bullit')
Then add it to the TimeFlow tf:
>>> tf.dateflow = df
Let’s see the cashflow as a timeflow:
>>> print tf
<instance TimeFlow>
Time Convertion:
Daycount method = act/365
Valuation date = 2009-11-22
Date Time Value
2009-11-22, 0.0000, 0.00
2009-11-24, 0.0055, 0.00
2010-11-24, 1.0055, 10.00
2011-11-24, 2.0055, 10.00
2012-11-24, 3.0055, 10.00
2013-11-24, 4.0055, 10.00
2014-11-24, 5.0055, 110.00
And now do some interest rate calculations:
>>> tf.npv_value(0) # The sum of the cashflow
Decimal('150.0000000000000000000000000')
>>> tf.npv_value(0.1) # The sum of the cashflow with discount rate 10%
Decimal('99.94778887869488654978784607')
>>> tf.npv_spread(100) # The Par rate
Decimal('0.09986242567998284995258866564')
Now set valuation date equal to the start of the cashflow:
>>> tf.valuation_date = '2009-11-24'
>>> print tf
<instance TimeFlow>
Time Convertion:
Daycount method = act/365
Valuation date = 2009-11-24
Date Time Value
2009-11-24, 0.0000, 0.00
2010-11-24, 1.0000, 10.00
2011-11-24, 2.0000, 10.00
2012-11-24, 3.0000, 10.00
2013-11-24, 4.0000, 10.00
2014-11-24, 5.0000, 110.00
Now the present value is 100:
>>> tf.npv_value(0.1) # The sum of the cashflow with discount rate 10%
Decimal('100.0000000000000000000000000')
And the spread becomes 10%:
>>> tf.npv_spread(100) # The Par rate should now be 10% or 0.1
Decimal('0.1000000000000000000000000002')
and the first and second derivative when the spread is 10%, respectively:
>>> tf.npv_d1(0.1)
Decimal('-379.0786769408448255521542866')
>>> tf.npv_d2(0.1)
Decimal('1936.834238279122197880851971')
There are the following standard interest rate risk calculation:
>>> tf.modified_duration(0.1)
Decimal('3.790786769408448255521542866')
>>> tf.macauley_duration(0.1)
Decimal('4.169865446349293081073697153')
>>> tf.modified_convexity(0.1)
Decimal('19.36834238279122197880851971')
>>> tf.macauley_convexity(0.1)
Decimal('23.43569428317737859435830885')
Value of a basis point, PVBP and PV01, refers to the average amount by which the MarkToMarket value of any instrument changes when the entire yield curve is shifted up and down by 0.01% (a basispoint). It is an absolute measure of pure price change.
pv01 and pvbp are methods in the object TimeFlow.
Below pv01 and pvbp are calculated at flat yieldcurve at 10% (0.1).
>>> tf.pv01(0.1)
Decimal('0.03790786769408448255521542866')
>>> tf.pvbp(0.1)
Decimal('0.03789818550933853843871350')
They are eg described in [Sadr]
It is possible to do decimal vector calculations here, eg:
>>> from decimalpy import round_decimal
>>> rates = [0.05, 0.075, 0.1, 0.125, 0.15]
>>> [str(round_decimal(npv, 2)) for npv in tf.npv_value(rates)]
['121.65', '110.11', '100.00', '91.10', '83.24']
or:
>>> [str(round_decimal(spread, 4)) for spread in tf.npv_spread([90, 100, 110])]
['0.1283', '0.1000', '0.0753']
or:
>>> [str(round_decimal(npv, 4)) for npv in tf.modified_duration(rates)]
['4.0510', '3.9183', '3.7908', '3.6683', '3.5504']
So scenarios and grafs becomes quite easy.
| Parameters: | spread (A float between 0 and 1) – A rate based generel spread. |
|---|---|
| Returns: | First order derivative for the DateFlow and time valuation parameters given at instantiation |
Formula for npv_d1:
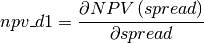
| Parameters: | spread (A float between 0 and 1) – A rate based generel spread. |
|---|---|
| Returns: | Second order derivative for the DateFlow and time valuation parameters given at instantiation |
Formula for npv_d2:
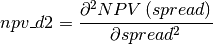
| Parameters: |
|
|---|---|
| Returns: | The par rate of the discounted cashflow |
| Parameters: |
|
|---|---|
| Returns: | npv_value for the DateFlow and time valuation parameters given at instantiation |
Short hand notation for npv_value in the documentation:
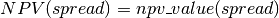
Note
Actually when no discountcurve is used the spread can be used to implement the discountcurve with constant discountfactor for each future period of fixed length.
The module finance.yieldcurves
All that needs to be added in order to implement is one or more yieldcurve functions to be used for the calculations and set the __init__ method for the new yieldcurve.
The FinancialCubicSpline is the spline where the curvatures are set to 0 at extrapolation. This means that the extrapolation is a horizontal straight line at the endpoint far to the right.
Instantiated by:
| Parameters: |
|
|---|
How to use:
Instantiate:
>>> import finance
>>> times = [0.5, 1, 2, 4, 5, 10, 15, 20]
>>> rates = [0.0552, 0.06, 0.0682, 0.0801, 0.0843, 0.0931, 0.0912, 0.0857]
>>> fcs = finance.yieldcurves.FinancialCubicSpline(times, rates)
See the settings:
>>> fcs
Financial cubic spline based on points:
.. (0.5000, 0.0552)
.. (1.0000, 0.0600)
.. (2.0000, 0.0682)
.. (4.0000, 0.0801)
.. (5.0000, 0.0843)
.. (10.0000, 0.0931)
.. (15.0000, 0.0912)
.. (20.0000, 0.0857)
This yield curve is right continous and piecewise constant. The curve is instantiated by a set of right endpoints for each step in the curve. If time 0 isn’t present in the set of times the point (0, 0) is added.
Instantiated by:
| Parameters: |
|
|---|
How to use:
Instantiate:
>>> import finance
>>> times = [0.5, 1, 2, 4, 5, 10, 15, 20]
>>> rates = [0.0552, 0.06, 0.0682, 0.0801, 0.0843, 0.0931, 0.0912, 0.0857]
>>> li = finance.yieldcurves.LinearSpline(times, rates)
See the settings:
>>> li
Linear interpolation curve based on points:
.. (0.0000, 0.0000)
.. (0.5000, 0.0552)
.. (1.0000, 0.0600)
.. (2.0000, 0.0682)
.. (4.0000, 0.0801)
.. (5.0000, 0.0843)
.. (10.0000, 0.0931)
.. (15.0000, 0.0912)
.. (20.0000, 0.0857)
>>> print li.continous_forward_rate(times[:4])
Vector([0.0552, 0.0600, 0.0682, 0.0801])
Getting the slope of the continous forward rate at time 1 (at a jump) and at time 1.1:
>>> print li.continous_rate_timeslope([1, 1.1])
Vector([0.0089, 0.0082])
Getting the instantanous forward rate at time 1 (at a jump) and at time 1.1:
>>> print li.instantanious_forward_rate([1, 1.1])
Vector([0.0689, 0.06984])
The NaturalCubicSpline is the spline where the curvatures are set to 0 at extrapolation. This means that the extrapolation is a straight line with slope as the one at endpoints.
Instantiated by:
| Parameters: |
|
|---|
How to use:
Instantiate:
>>> import finance
>>> times = [0.5, 1, 2, 4, 5, 10, 15, 20]
>>> rates = [0.0552, 0.06, 0.0682, 0.0801, 0.0843, 0.0931, 0.0912, 0.0857]
>>> ncs = finance.yieldcurves.NaturalCubicSpline(times, rates)
See the settings:
>>> ncs
Natural cubic spline based on points:
.. (0.5000, 0.0552)
.. (1.0000, 0.0600)
.. (2.0000, 0.0682)
.. (4.0000, 0.0801)
.. (5.0000, 0.0843)
.. (10.0000, 0.0931)
.. (15.0000, 0.0912)
.. (20.0000, 0.0857)
Getting the continous forward rate:
>>> print ncs.continous_forward_rate(times[:3])
Vector([0.05520000000000000000000000000, 0.06000000000000000000000000000, 0.06820000000000000000000000000])
Getting the slope of the continous forward rate at time 1
>>> print ncs.continous_rate_timeslope(1)
0.009216950866030399434428966667
Getting the instantanous forward rate at time 1
>>> print ncs.instantanious_forward_rate(1)
0.06921695086603039943442896667
The Nelson Siegel defined with a level, slope, curvature and scale parameters.
Instantiated by:
| Parameters: |
|
|---|
How to use:
Instantiate:
>>> import finance
>>> ns = finance.yieldcurves.NelsonSiegel(0.061, -0.01, -0.0241, 0.275)
See the settings:
>>> ns
Nelson Siegel (level=0.061, slope=-0.01, curvature=-0.0241, scale=0.275)
Get the discountfactors at times 1, 2, 5, 10:
>>> times = [1, 2, 5, 10]
>>> ns(times)
Vector([0.9517121708497056177816078083, 0.9072377300179418172521412527, 0.7844132592062346545344544940, 0.6008958407659500402742872859])
Get the zero coupon rate at time 5 and 7
>>> r5, r7 = ns.zero_coupon_rate([5, 7])
>>> r5, r7
(Decimal('0.049762403554685553400657196'), Decimal('0.050625188777310061599365592'))
Get the forward rate between time 5 and 7
>>> f5_7 = ns.discrete_forward_rate(5, 7)
>>> f5_7
Decimal('0.052785255470657667493924028')
Verify the results:
>>> (1 + r5) ** 5 * (1 + f5_7) ** 2
Decimal('1.412975598166187290121638358')
>>> (1 + r7) ** 7
Decimal('1.412975598166187290121638354')
Only the last decimal differ!
| Parameters: | t_value (a positive integer, float or decimal) – A time value |
|---|---|
| Returns: | The curvature in a nelson Siegel curve at time t_value |
| Parameters: | t_value (a positive integer, float or decimal) – A time value |
|---|---|
| Returns: | The Level in a nelson Siegel curve at time t_value |
| Parameters: | t_value (a positive integer, float or decimal) – A time value |
|---|---|
| Returns: | The Slope in a nelson Siegel curve at time t_value |
This yield curve is right continous and piecewise constant. The curve is instantiated by a set of right endpoints for each step in the curve. If time 0 isn’t present in the set of times the point (0, 0) is added.
Instantiated by:
| Parameters: |
|
|---|
How to use:
Instantiate:
>>> import finance
>>> times = [0.5, 1, 2, 4, 5, 10, 15, 20]
>>> rates = [0.0552, 0.06, 0.0682, 0.0801, 0.0843, 0.0931, 0.0912, 0.0857]
>>> pc = finance.yieldcurves.PiecewiseConstant(times, rates)
See the settings:
>>> pc
Piecewise constant curve based on points:
.. (0.0000, 0.0000)
.. (0.5000, 0.0552)
.. (1.0000, 0.0600)
.. (2.0000, 0.0682)
.. (4.0000, 0.0801)
.. (5.0000, 0.0843)
.. (10.0000, 0.0931)
.. (15.0000, 0.0912)
.. (20.0000, 0.0857)
>>> print pc.continous_forward_rate(times[:4])
Vector([0.0552, 0.06, 0.0682, 0.0801])
Getting the slope of the continous forward rate at time 1 (at a jump) and at time 1.1:
>>> print pc.continous_rate_timeslope([1, 1.1])
Vector([47.83333333333333333333333333, 0])
Getting the instantanous forward rate at time 1 (at a jump) and at time 1.1:
>>> print pc.instantanious_forward_rate([1, 1.1])
Vector([47.89333333333333333333333333, 0.0682])
CummutativeAddition is a meta class for handling cummutative addition.
Usage
Define a class with the necessary and suffient methods:
>>> class cummutative_addition(CummutativeAddition):
... def __init__(self, value):
... self.value = str(value)
... def __neg__(self):
... return 'neg(%s)' % self.value
... def __abs__(self):
... return 'abs(%s)' % self.value
... def __add__(self, value):
... return self.value + str(value)
... def __rsub__(self, value):
... return '%s + %s' % (str(value), -self)
...
Let’s instanciate the class:
>>> test = cummutative_addition(5)
Now cummulative addition is possible. First left addition as defined above:
>>> test + 4
'54'
Right addition is the same as left, but is defined through the parent class:
>>> 4+test # = test + 4 since the addition is cummutative
'54'
What is understood by the function abs and by the negative value has to be defined in each cummutative additive class:
>>> abs(test)
'abs(5)'
>>> -test
'neg(5)'
Subtraction is also defined as addition where one or more elements are negative:
>>> test-4
'5-4'
>>> 4-test
'4 + neg(5)'
>>> test += 1
>>> test
'51'
If not all necessary methods are defined an error is raised. Below is such a class:
>>> class not_all_methods_defined(CummutativeAddition):
... def __init__(self, value):
... self.value = str(value)
... def __add__(self, value):
... return self.value + str(value)
... def __rsub__(self, value):
... pass
...
And the error the class raises:
The abstractmethod decorated methods must be defined: >>> try: ... test = not_all_methods_defined(5) ... except Exception, error_text: ... print error_text ... Can’t instantiate abstract class not_all_methods_defined with abstract methods __abs__, __neg__
Multiplication is a meta class for handling cummutative multiplication.
Usage
This is basically the same as cummutative addition. Let’s look at a class:
>>> class cummutative_multiplication(CummutativeMultiplication):
... def __init__(self, value):
... self.value = str(value)
... def __mul__(self, value):
... return '%s * %s' % (self.value, value)
... def __div__(self, value):
... return '%s / %s' % (self.value, value)
... def __rdiv__(self, value):
... return '%s / %s' % (value, self.value)
...
Instantiation of that class:
>>> test = cummutative_multiplication(5)
Left multiplication as defined in the class:
>>> test * 4
'5 * 4'
Right multiplication as inherited:
>>> 4*test # = test * 4 since the multiplication is cummutative
'5 * 4'
Both left and right division has to be defined in the class:
>>> test / 4
'5 / 4'
>>> 4/test # != test / 4 since the division is not cummutative
'4 / 5'
Power is a meta class for handling the power of an object.
Usage
This is basically the same as cummutative additiion. Let’s look at a class:
>>> class power(Power):
... def __init__(self, value):
... self.value = str(value)
... def __pow__(self, value):
... return '%s ** %s' % (self.value, value)
... def __rpow__(self, value):
... return '%s ** %s' % (value, self.value)
...
Instantiation of that class:
>>> test = power(5)
Left and right power has been defined in the class:
>>> test ** 4
'5 ** 4'
>>> 4**test
'4 ** 5'
Self power is inherited:
>>> test **= 3
>>> print test
5 ** 3
| download: | the SimpleTk module |
|---|
The code is open source under the Python Software Foundation License
Scripting in VBA/Excel have tought me that you get a long way using simple dialogs.
For a long while I’ve never had the need to use dialogs in my Python coding. When I did, I found that by accident the set of simple dialog functions spread out into 4 separate modules.
This module unites all simple ask functions from the python modules:
- tkMessageBox
- tkSimpleDialog
- tkColorChooser
- tkFileDialog
into one single class SimpleDialogTk.
When my usage of dialogs in VBA/Excel went a bit further it had usually to do with using a set of simple labelled input elements to get a set of values.
I was inspired by EasyGUI. The idea of hiding the eventdriven principle of tkinter and reduce the GUI to a matter of calling the GUI functions and getting the input values (the code being linear).
I just want to get the input values for use in the Python code.
My solution consist of the following classes:
- BaseRoot - Usually it is needed to have the possibility of accepting or cancel the input data. That decision is kept in the property input_ok
- LabelledEntry - A labelled entry field. Return a string
- LabelledList - A labelled single select listbox. Return a string
- LabelledCheckButton - A CheckButton build on the same ideas as LabelledEntry and LabelledList
Common to all the labelled classes above is that when they are called as functions they return the value set in the GUI.
To see the code in action there is the following example of an login window:
1 2 3 4 5 6 7 8 9 10 11 | master = BaseRoot('Example of advanced QaDdialog, login')
user_name = LabelledEntry(master(), 'Enter username:', 'MyUserName')
password = LabelledEntry(master(), 'Enter password:', get_focus=True, show='*')
server_names = ['Server%02d' % i for i in range(12)]
server = LabelledList(master(), 'Choose server:', server_names)
advanced = LabelledCheckButton(master(), 'Advanced login')
master().mainloop()
if master.input_ok:
print 'Login with: ', user_name(), password(), server(), advanced()
else:
print 'Login ignored', user_name(), password(), server(), advanced()
|
which results in the following GUI (Ubuntu 13.04):
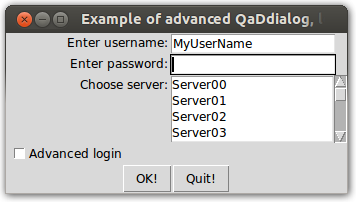
Commenting the example code above:
- line 1: Regrettably we still has to use an root element. Here the window title is set
- line 2: The typical arguments for a labelled entry are master, label text and a start value (my own login)
- line 3: If I like the default login there is no need to start at login, so focus is set to the password entry. Also the password is not to be shown. It will be hidden behind show character
- line 4: Create a list of server names
- line 5: Choose server to use from the list of server names
- line 6: It is also possible simply to check things off using a check button
- line 7: The master returns a root element when called as a function. In order to get data one must call the method mainloop of the root
- line 8: Here it is assumed that the window is closed again. If the window is closed with the ok button then the property input_ok of the master is true, otherwise it is false. This way one can control wether or not to use the entered data
- line 9-: Here it is assumed that the window is closed again. When the input instances are called as functions they return their contents as string, except for LabelledCheckButton which returns 0 or 1
BaseRoot is basically a base frame with 2 buttons, OK and Quit. Pressing the buttons closes the window again.
Whether the OK or the Quit button is pressed is kept in the property input_ok.
When called as a function it returns a tkinter Tk root element. The mainloop method of this element must be called in order to get the input from the user.
| Parameters: | master_title (A string value) – Title text of the base window |
|---|
A check button that keeps its input. A building block for simple GUIs. Requires an instance of a BaseRoot class as input. After the BaseRoot class instance is closed the entered value can be retrieved by calling the instance of the LabelledCheckButton.
A labelled entry. A building block for simple GUIs. Requires an instance of a BaseRoot class as input. After the BaseRoot class instance is closed the entered value can be retrieved by calling the instance of the LabelledEntry.
| Parameters: |
|
|---|
A labelled single select listbox. A building block for simple GUIs. Requires an instance of a BaseRoot class as input. After the BaseRoot class instance is closed the entered value can be retrieved by calling the instance of the LabelledList.
| Parameters: |
|
|---|
SimpleDialogTk is a class containing all simple dialog functions in python. It unites all simple ask functions from the following python modules:
- tkMessageBox
- tkSimpleDialog
- tkColorChooser
- tkFileDialog
The functions are:
- askcolor - Ask for a color
- askdirectory - Ask for a directory, and return the file name
- askfloat - get a float from the user. Arguments are mainly title, the dialog title, and prompt, the label text. The return value is a float
- askinteger - get an integer from the user. Arguments are mainly title, the dialog title, and prompt, the label text. The return value is an integer
- askokcancel - Ask if operation should proceed; return true if the answer is ok
- askopenfile - Ask for a filename to open, and returned the opened file. File mode can be set, default is ‘r’
- askopenfilename - Ask for a filename to open
- askopenfilenames - Ask for multiple filenames to open. Returns a list of filenames or empty list if cancel button selected
- askopenfiles - Ask for multiple filenames and return the open file objects. Returns a list of open file objects or an empty list if cancel selected. File mode can be set, default is ‘r’
- askquestion - Ask a question. Arguments are mainly title and message
- askretrycancel - Ask if operation should be retried; return true if the answer is yes. Arguments are mainly title and message
- asksaveasfile - Ask for a filename to save as, and returned the opened file. File mode can be set, default is ‘w’
- asksaveasfilename - Ask for a filename to save as
- askstring - get a string from the user. Arguments are mainly title, the dialog title, and prompt, the label text. Return value is a string
- askyesno - Ask a question; return true if the answer is yes. Arguments are mainly title and message
- askyesnocancel - Ask a question; return true if the answer is yes, None if cancelled. Arguments are mainly title and message
- showerror - Show an error message. Arguments are mainly title and message
- showinfo - Show an info message. Arguments are mainly title and message
- showwarning - Show a warning message. Arguments are mainly title and message
To use the functions just do:
>>> from SimpleTk import SimpleDialogTk
>>> ask = SimpleDialogTk()
>>> print ask.askyesno('Demo of SimpleDialogTk', 'Do you like what you see?')
It results in (Ubuntu 13.04):
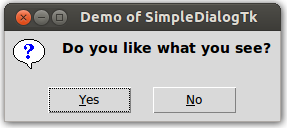
printing either True or False depending on your answer.
Build a menu from a dictionary
Usage
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 | import SimpleTk
from collections import OrderedDict as odct
root = SimpleTk.tk.Tk()
menubar = SimpleTk.tk.Menu(root, tearoff=0)
dialogs = SimpleTk.SimpleDialogTk()
def quit_and_destroy(): root.destroy(); root.quit()
submenu_dct = odct([
('Say hi 1', lambda: dialogs.askokcancel('Test1', 'Say HI!')),
('Say hi 2', lambda: dialogs.askokcancel('Test2', 'Say HI!'))
])
menu_dct = odct([
('Say hi menu', submenu_dct),
#('separator', None), does not work
('Close', quit_and_destroy)
])
SimpleTk.build_menu_from_dict(menu_dct, menubar)
root.config(menu=menubar)
root.mainloop()
print 'done'
|